A 2D model is created. Plane elements and beam elements are used to discretize rubber material and carbon fiber, respectively. To ensure that rubber and carbon fiber deform together (no slipping), plane elements and beam elements share common nodes. A concentrated force (the red arrow in Fig.1) is applied in ten load steps. Due to the hyperelastic material behavior of rubber, large deflection should be turned on. 3-parameter Mooney-Rivlin data table is activated.

FINISH
/CLEAR
/FILNAME,MODEL 1
/TITLE, MODEL 1

!Hyperelastic: Mooney-Rivlin material model, density=1240 kg/m^3, poisson=0.323
!carbon fibre, E=2.28E11Pa, density=1800kg/m^3, poisson=0.23

*SET,DIA,0.003		!the diameter of carbon fibre

/PREP7
ET,1,PLANE183,1,,2		!plane strain
MP,PRXY,1,0.323		!define the properties of rubber
MP,DENS,1,1240
TB,HYPER,1,,3,MOONEY     	!Activate 3 parameter Mooney-Rivlin data table
TBDATA,1,0.163498        	!Define c10
TBDATA,2,0.125076        	!Define c01
TBDATA,3,0.014719        	!Define c11
TBDATA,4,6.93063E-5      	!Define incompressibility parameter as 2/K, K is the bulk modulus
!!!!!!!!!!!!!!!!!!!!!!!!!
ET,2,BEAM3
MP,EX,2,2.28E11
MP,PRXY,2,0.23
MP,DENS,2,1800
R,2,2*ASIN(1)*(DIA/2)**2,2*ASIN(1)*DIA**4/64,DIA

!create the geometry
K,1,
K,2,0.1,
K,3,0.1,0.1
K,4,0,0.1
L,1,2
L,2,3
L,1,3
L,3,4
L,4,1
AL,1,2,3
AL,3,4,5
AGLUE,1,2

!mesh the geometry
!beam elements and plane elements share common nodes (deform together)
LSEL,S,,,3
LATT,2,2,2
LESIZE,ALL,,,100
LMESH,ALL		!beam elements
ALLSEL
LSEL,S,,,1,2,1
LESIZE,ALL,,,50
ALLSEL
LSEL,S,,,4,5,1
LESIZE,ALL,,,50
ALLSEL
LCCAT,1,2
LCCAT,4,5
ASEL,S,,,1,2,1
AATT,1,,1
MSHAPE,1,2D
MSHKEY,2
AMESH,ALL		!plane elements
ALLSEL

!boundary conditions
NSEL,S,LOC,X,0.1
NSEL,R,LOC,Y,0
CM,FIXED,NODE
D,ALL,ALL		!fixed support
ALLSEL
NSEL,S,LOC,X,0,0.1
NSEL,R,LOC,Y,0
NSEL,U,,,FIXED
DSYM,SYMM,Y,0		!symmetric boundary
ALLSEL
NSEL,S,LOC,X,0.1
NSEL,R,LOC,Y,0,0.1
NSEL,U,,,FIXED
DSYM,SYMM,X,0		!symmetric boundary
ALLSEL

/SOLU
ANTYPE,0
NLGEOM,ON
*DO,I,1,10
TIME,I
NSUBST,30,30,20,ON
KBC,0
OUTRES,ALL,ALL
FK,3,FY,-10*I
SFTRAN
ALLSEL
SOLVE
*ENDDO

/POST26
NSEL,S,LOC,X,0.1
NSEL,R,LOC,Y,0.05
*GET,NODENUM,NODE,0,NUM,MAX,	!get the node number
ANSOL,2,NODENUM,S,Y,STRESSY	!get the y-stress of this node
ANSOL,3,NODENUM,S,1,STRESS1	!get the 1st principal stress
ANSOL,4,NODENUM,S,EQV,STRESSEQV	!the equivalent stress
ANSOL,5,NODENUM,EPEL,Y,ESTRAINY		!y-elastic-strain
ANSOL,6,NODENUM,EPPL,Y,PSTRAINY		!y-plastic-strain
ADD,7,5,6		!elastic strain + plastic strain
ADD,8,7,,,,,,-1		!change the sign of variable 7
ADD,9,2,,,,,,-1		!change the sign of variable 2
/AXLAB,X,STRAIN
/AXLAB,Y,STRESS[Pa]
XVAR,7
PLVAR,2
/AXLAB,X,STRAIN
/AXLAB,Y,STRESS[Pa]
XVAR,8
PLVAR,9

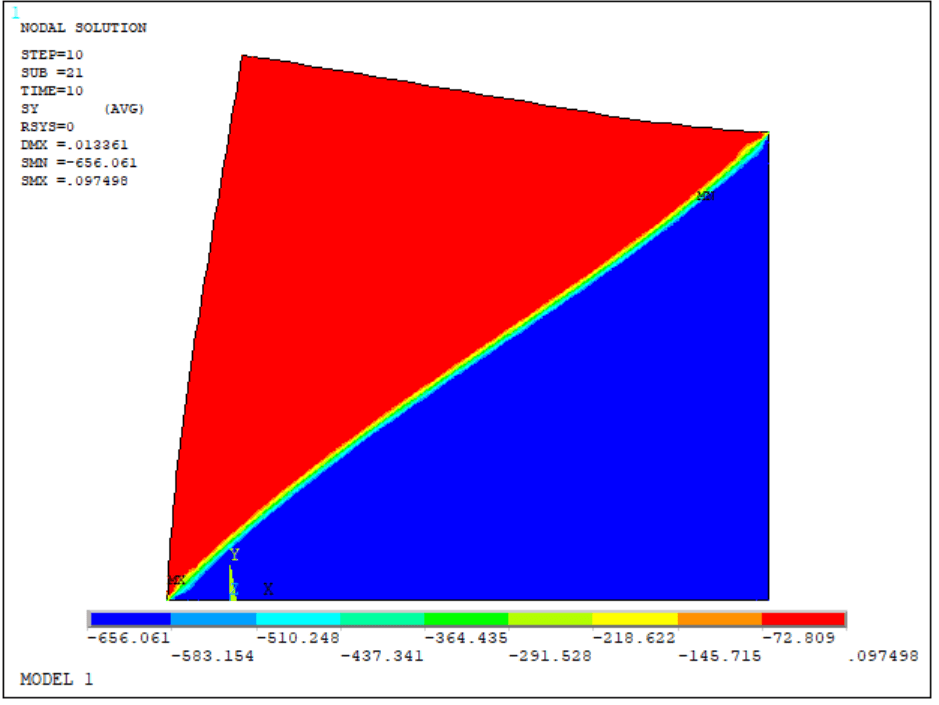
Fig. 4. Stress-strain curve (sampled in the middle of the right edge)