Typical piston rubber films in a pneumatic brake device that is commonly used in drilling operations are shown in Fig.1-Fig.3. When the brake device is activated, the piston rubber film deforms under increasing air pressure and pushes the brake lever forward to achieve braking. 

Fig.4. The cross section of the rubber film.

Some features of this problem:

• The rubber film is an axisymmetric structure. 
• The hyperelastic behavior of rubber material means large deflection should be turned on. Mooney-Rivlin material model is used.
• Both displacement boundary conditions and stress boundary conditions are involved. More details can be found in the following APDL.

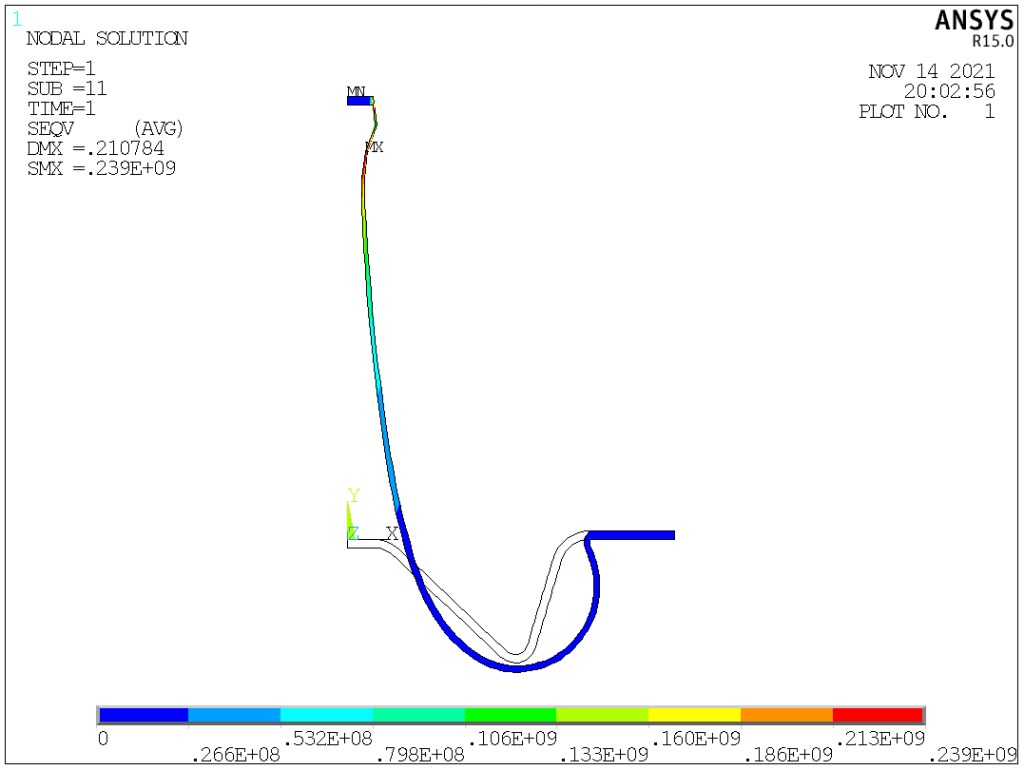
FINISH
/CLEAR
!*************************************
!units: m, N, Pa
!define parameters
!*************************************
ADD_R=0.005		!the increased radius of the central part
EDGE_R=0.151+ADD_R	!the radius of the edge
OUT_R=0.1+ADD_R	        !the outer radius of the central part
IN_R=0.06+ADD_R		!the inner radius of the central part
R_HOLE=0.02		!the radiu of the central hole
H_RIDGE=0.05		!height
THICK=0.008		!thickness
RR_RIDGE=0.006		!the radius of fillet 1
RR_IN=0.018		!the radius of fillet 2
PI=2*ASIN(1)
F_ANTI=11300		!the force that is exerted on the rubber film by brake lever
PRES_UP=0.637E6		!the braking air pressure
!*************************************
WID_EDGE=EDGE_R-OUT_R
WID_CAP=IN_R-R_HOLE
R_RIDGE=(OUT_R+IN_R)/2
WID_RIDGE=(OUT_R-IN_R)/2
THETA=ATAN((H_RIDGE-THICK)/WID_RIDGE)
THIN=THICK/COS(THETA)
DELTA=THICK*TAN(PI/2-THETA)
KYY=-H_RIDGE-THICK/2-((RR_RIDGE+THICK/2)/SIN(PI/2-THETA)-(RR_RIDGE+THICK/2))

!*************************************
!create geometry
!*************************************
/PREP7
K,1,0,-THICK/2,0
K,2,0,-THICK/2,0
K,3,RR_IN,-THICK/2,0
K,4,R_RIDGE,KYY,0
K,5,OUT_R,0,0
K,6,EDGE_R,0,0
LSTR,2,3			!define a straight line
LSTR,3,4
LSTR,4,5
LSTR,5,6
LFILLT,1,2,RR_IN-THICK/2	!generates a fillet line between two intersecting lines
LFILLT,2,3,RR_RIDGE+THICK/2
LFILLT,4,3,RR_IN-THICK/2
KL,6,0.5,101		!generate a keypoint at a specified location on an existing line
K,13,0,0,0
K,14,0,-THICK/2,0
LSTR,13,14
FLST,8,7,4		!http://www.ansysjgy.com/index.php/2021/07/12/fa6c797878/
FITEM,8,1
FITEM,8,5
FITEM,8,2
FITEM,8,6
FITEM,8,3
FITEM,8,7
FITEM,8,4
ADRAG,8,,,,,,P51X	!drag line8 along the path defined by line 1,5,2,6,3,7,4

!*************************************
!define element and material property
!*************************************
ET,1,HYPER56		!2D 4-node mixed U-P hyperelastic solid element
			!http://research.me.udel.edu/~lwang/teaching/MEx81/ansys56manual.pdf
			!https://www.wenjiangs.com/doc/0aqjwbuq
KEYOPT,1,3,1		!axisymmetric
MP,EX,1,3.25E6
MP,NUXY,1,0.49967
TB,MOONEY,1
TBDATA,1,1.6E6		!yield strength
TBDATA,2,0.81E6		!shear modulus
R_DOWN=KX(16)
PRES_DOWN=F_ANTI/(PI*R_DOWN**2)	!calculate the stress from the brake lever

!*************************************
!mesh
!*************************************
AESIZE,ALL,0.002
MSHAPE,0,2D
MSHKEY,1
AMESH,ALL
FINISH

/SOLU
!*************************************
!displacement BCs
!*************************************
DL,8,,SYMM		!symmetric boundary
DA,7,ALL		!the area fixed by bolts
DA,1,UX
ASEL,S,AREA,,1,,
NSLA,S,1
CP,1,UY,ALL		!couple the y-deformation of all nodes on area 1(because of the prensence of braking rod)
CPSGEN,1,UY		!generates sets of coupled nodes from existing sets
ALLSEL
!*************************************
!stress BCs
!*************************************
LSEL,S,LINE,,10,25,3
SFL,ALL,PRES,PRES_UP	!apply braking are pressure
ALLSEL
SFL,11,PRES,PRES_DOWN	!apply the stress from braking rod
LSEL,S,LINE,,14,26,3
SFL,ALL,PRES,0.1E6	!apply atmospheric pressure
ALLSEL
ANTYPE,0
NLGEOM,1		!turn on large deflection
NSUBST,5,0,0
OUTRES,,1
SOLVE

/POST1
PLNSOL,S,EQV,2,1

Fig.7. Area number.

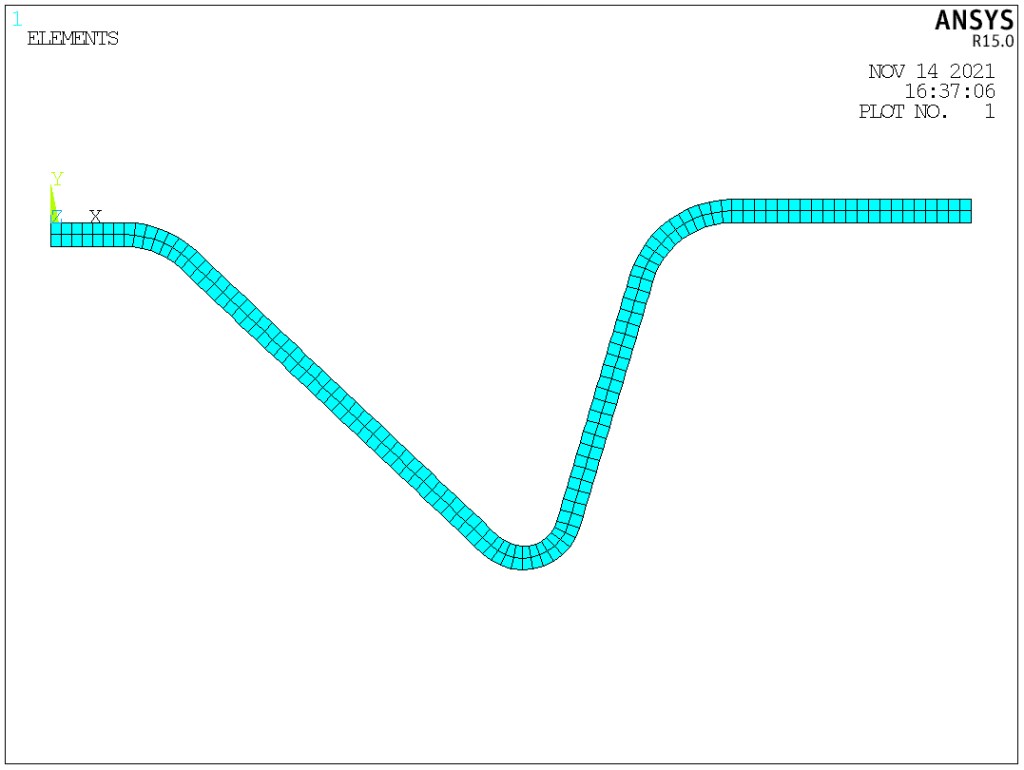
Fig.8. Discretization.