A two-spring system is subjected to a force F as shown below. l=10 cm, k1=8N/cm, and k2=1N/cm. F=5*2^0.5N. Determine the strain energy of the system and the displacements δx and δy.

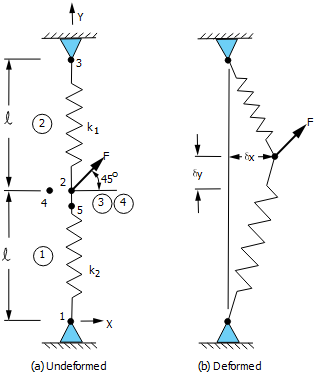
The solution to this problem is best obtained by adding mass and using the “slow dynamics” technique with approximately critical damping. Combination elements (COMBIN40) are used to provide damping in the X and Y directions. Approximate damping coefficients Cx and Cy, in the x and y directions respectively, are determined from

where m is arbitrarily assumed to be unity. kx and ky cannot be known before solving so are approximated by Ky=K2=1N/cm and Kx=Ky/2=0.5N/cm, hence Cx = 1.41 and Cy = 2.0. Large deflection analysis is performed due to the fact that the resistance to the load is a function of the deformed position. The APDL is as follows.

FINISH
/CLEAR
/PREP7
/TITLE, LARGE LATERAL DEFLECTION OF UNEQUAL STIFFNESS SPRINGS
/COM, REF: G.N. VANDERPLAATS, "NUMERICAL OPTIMIZATION TECHNIQUES FOR
/COM,      ENGINEERING DESIGN", PP 72-73, MCGRAW-HILL, 1984
ET,1,COMBIN14,,,2          !2-D longitudinal spring-damper
ET,3,COMBIN40,,,,,,2       !UX displacement along nodal X axis, all mass is at node j
ET,4,COMBIN40,,,2,,,2      !UY displacement along nodal Y axis, all mass is at node j
R,1,1                      !spring stiffness=1
R,2,8                      !spring stiffness=8
/COM use COMBIN40 mass, k, and damping c, to approximate critical damping
R,3,,1.41,1                !c=1.41, m=1
R,4,,2,1                   !c=2, m=1
N,1
N,2,,10
N,3,,20
N,4,-1,10
N,5,,9
E,1,2                      !element 1 is spring element with stiffness 1
REAL,2
E,2,3                      !element 2 is spring element with stiffness 8
TYPE,3
REAL,3
E,4,2                      !element 3 is combination element with c=1.41
TYPE,4
REAL,4
E,5,2                      !element 4 is combination element with c=2
NSEL,U,NODE,,2
D,ALL,ALL
NSEL,ALL
FINISH
/SOLU    
ANTYPE,TRANS               !full transient dynamic analysis
NLGEOM,ON                  !turn on large deflection
KBC,1                      !stepped load
F,2,FX,5
F,2,FY,5
AUTOTS,ON
NSUBST,30
OUTPR,,LAST
OUTPR,VENG,LAST		   !element energies
TIME,15                    !arbitrary time for slow dynamics (time at the end of the load step)
/OUT,SCRATCH
SOLVE
FINISH
/POST1
SET,,,,,15                 !when time=15
/OUT,
ETABLE,SENE,SENE           !the table storing strain energy
SSUM                       !calculates and prints the sum of element table items
*GET,ST_EN,SSUM,,ITEM,SENE
PRNSOL,U,COMP              !print displacements in global coordinate system
*GET,DEF_X,NODE,2,U,X
*GET,DEF_Y,NODE,2,U,Y

This APDL is posted as I saw this paper: Experimental and numerical investigation of a vertical vibration isolator for seismic applications. They designed a vibration isolator consisting of multiple springs.

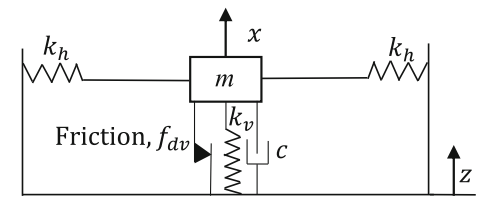
The APDL in this post provides a start point to model an experiment rig like this.