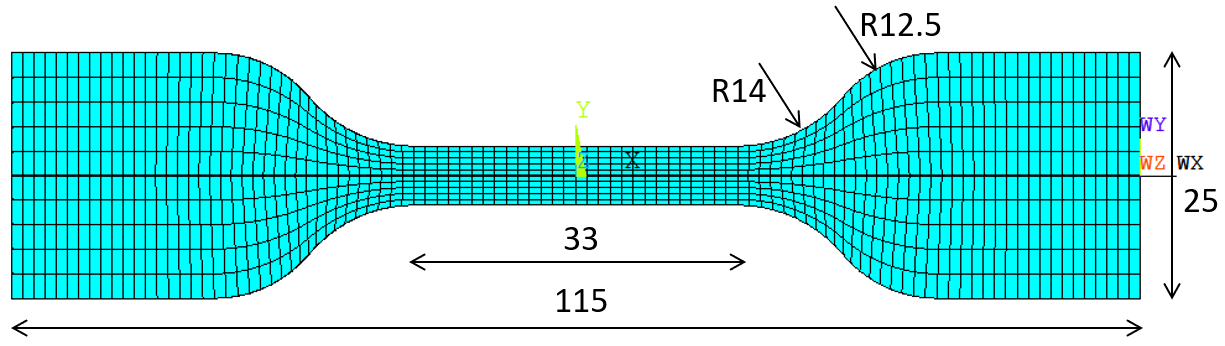
This example shows the static analysis of a tensile test sample made of rubber. The dimensions of the sample are shown in the following figure. The thickness of the sample is 1.5mm. Using the symmetry, only 1/8 of the sample is analyzed. After solving the 1/8 model, the results of the full model can be shown using /EXPAND.

Rubber material is modeled using the 3-term Yeoh model. C10=0.6976MPa, C20=-0.24484MPa, and C30=0.12629MPa. The incompressibility parameter is 0. A displacement of 19.14mm is applied to the end of the sample. After the calculation, a force-displacement curve is obtained. The tensile force is calculated by collecting the reaction forces of those nodes to which a displacement constraint is applied. A *DO loop is used to achieve this.

The APDL of this example is as follows (annotations are in lowercase).

FINISH
/CLEAR
!units: mm, MPa
LENG_OVERALL=115
LENG_CENTER=33
THICK=1.5
WID_CENTER=6
RAD_LARGE=25/2
RAD_SMALL=14
WID_OVERALL=2*RAD_LARGE
*AFUN,DEG		!specifies units for angular functions in parameter expressions
/PREP7
ET,1,SOLID185
KEYOPT,1,6,1	!element formulation: mixed formulation (using displacement and hydrostatic pressure as primary unknowns to avoid volumetrix locking for incompressible materials)
R,1
TB,HYPE,1,1,3,YEOH
TBTEMP,0
TBDATA,,0.6976,-0.24484,0.12629
!!create geometry:
RECTNG,,LENG_CENTER/2,,WID_CENTER/2
ASEL,NONE
RECTNG,,LENG_OVERALL/2,,WID_OVERALL/2
WPOFFS,LENG_CENTER/2,WID_CENTER/2+RAD_SMALL
PCIRC,RAD_SMALL,,0,-90
CSWPLA,11,1
LSEL,S,LOC,X,RAD_SMALL
TEMPLINE1=LSNEXT(0)		!get the line number (next selected line having a line number greater than 0)
WPCSYS,-1,0
LENG_OFFSET=SQRT((RAD_SMALL+RAD_LARGE)**2-(RAD_SMALL+WID_CENTER/2)**2)
WPOFFS,LENG_CENTER/2+LENG_OFFSET
PCIRC,RAD_LARGE,,90,180
CSWPLA,12,1
LSEL,S,LOC,X,RAD_LARGE
TEMPLINE2=LSNEXT(0)
ADELE,ALL
LSEL,ALL
LOVLAP,TEMPLINE1,TEMPLINE2
CSYS,11
LSEL,S,LOC,Y,270,270+ATAN(LENG_OFFSET/(RAD_SMALL+WID_CENTER/2))
LSEL,R,LOC,X,RAD_SMALL
TEMPLINE1=LSNEXT(0)
CSYS,12
LSEL,S,LOC,Y,90,180-ATAN((RAD_SMALL+WID_CENTER/2)/LENG_OFFSET)
LSEL,R,LOC,X,RAD_LARGE
TEMPLINE2=LSNEXT(0)
LSEL,ALL
CSYS,0
ASEL,ALL
LSLA,U
LSEL,U,LOC,X,LENG_OVERALL/2
LSEL,U,LINE,,TEMPLINE1
LSEL,U,LINE,,TEMPLINE2
LDELE,ALL,,,1
LSEL,ALL
NUMMRG,KP

A,2,6,7,12,15,3
WPCSYS,-1,0
KWPAVE,6
RECTNG,,-RAD_LARGE,,WID_OVERALL/2
AOVLAP,ALL
!!meshing and boundaries:
MSHAPE,0
MSHKEY,0
ESIZE,WID_CENTER/5
VEXT,ALL,,,0,0,THICK/2
VSWEEP,ALL
ASEL,S,LOC,X,0
DA,ALL,SYMM
ASEL,S,LOC,Y,0
DA,ALL,SYMM
ASEL,S,LOC,Z,0
DA,ALL,SYMM
DA,9,UX,0.58*LENG_CENTER
ALLSEL,ALL
FINISH

/SOLU
TIME,0.58*LENG_CENTER		!time=extension
NLGEOM,ON
OUTRES,ALL,ALL
NSUBST,20,1E3,20
ALLSEL,ALL
SOLVE
FINISH

/POST26
! !!calculate the overall reaction force:
ASEL,S,,,9
NSLA,S,1
*GET,nCount,NODE,,COUNT
nNow=0
*DO,I,1,nCount
	nNow=NDNEXT(nNow)
	RFORCE,2,nNow,F,X,TENSION
	ABS,3,2
	ADD,4,4,3
*ENDDO
PROD,5,4,,,,,,4		!the tension on the full model
PROD,6,1,,,,,,2		!the overall extention of the full model
/AXLAB,X,DISPLACEMENT (mm)
/AXLAB,Y,LOAD (N)
! /GROPT,REVY,1
!!plot the equilibrium path:
XVAR,6
PLVAR,5
FINISH

/POST1
ALLSEL
/EXPAND,2,RECT,HALF,0.00001,,,2,RECT,HALF,,0.00001,,2,RECT,HALF,,,0.00001  
PLNSOL,U,X,1
PLNSOL,S,1,1

1/8 model discretization

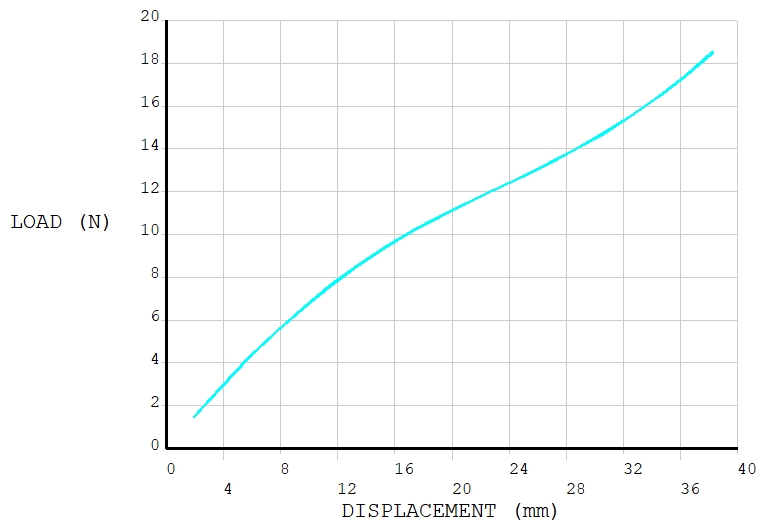
Equilibrium path

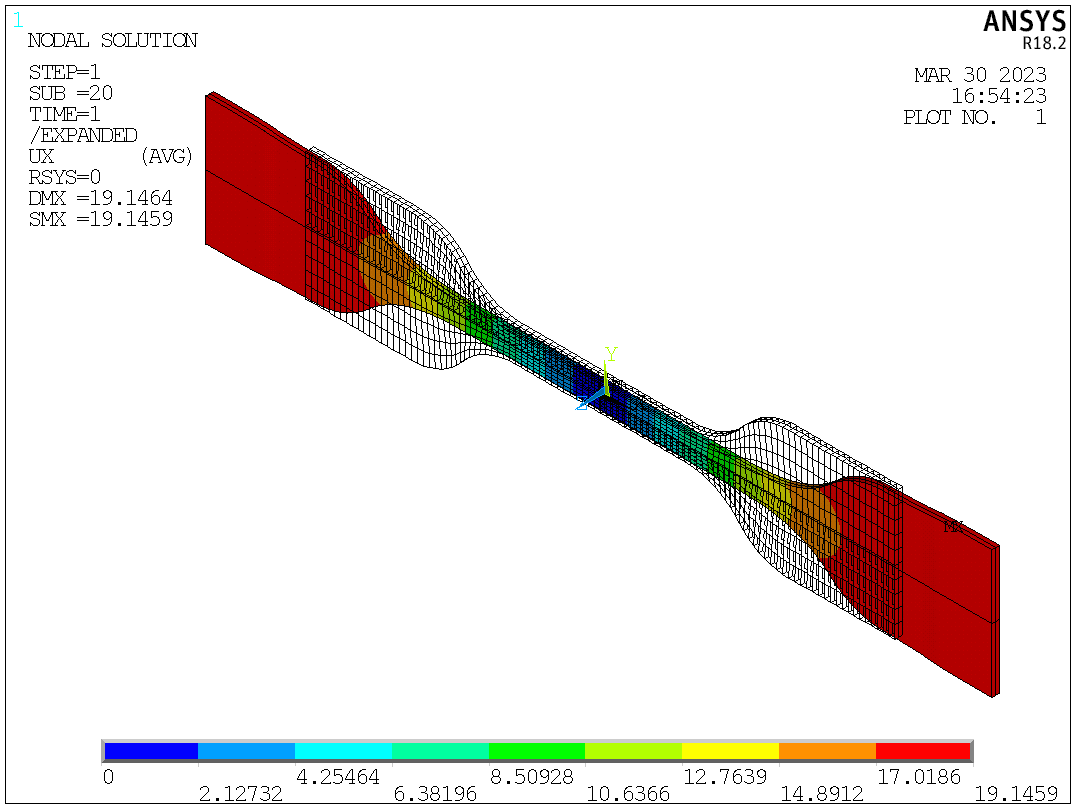
The displacement in X direction

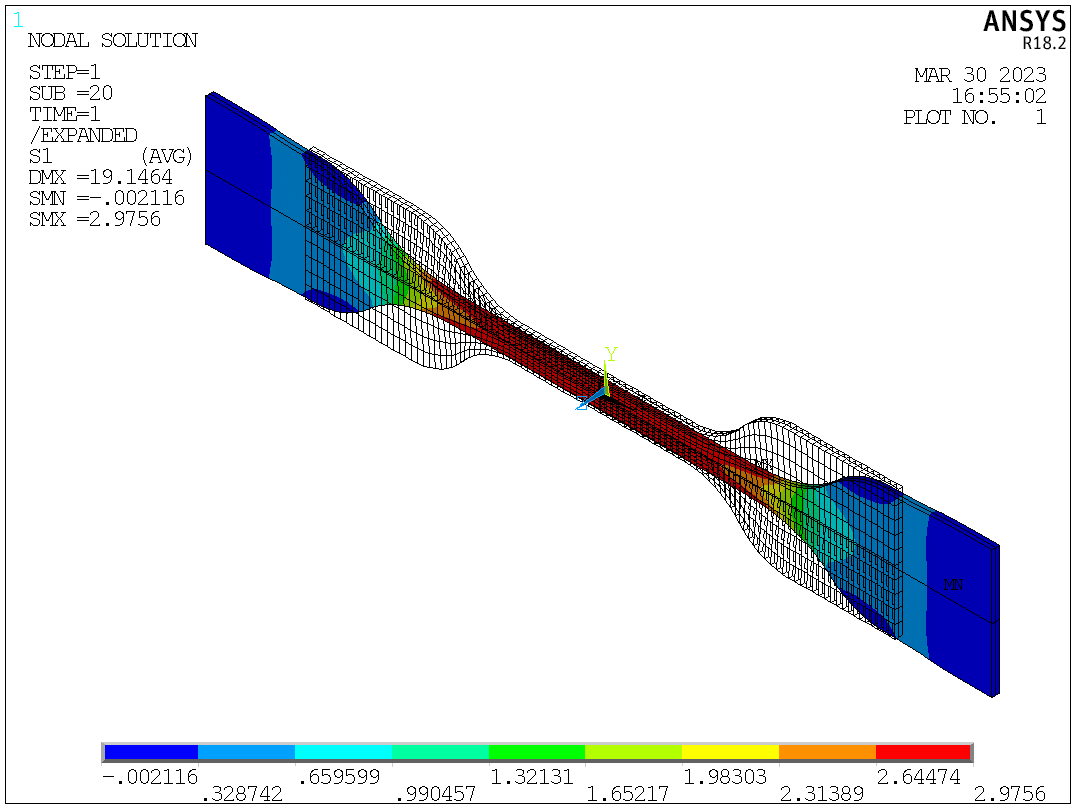
The distribution of the first principle stress

It should be noted that the stress and strain results exported from this model are true stress and true strain. To compare these results with experimental results, it is necessary to convert them to engineering stress and engineering strain. The relevant information can be found in ANSYS Help Viewer: