A structure can become unstable when a load reaches its buckling value or when nonlinear material becomes unstable. It is possible to observe the full response of a structure under proportional (ramped) loads using elastic-plastic analysis in ANSYS, so the plastic limit load and the location of plastic hinges can be determined. 

In this post, we will find the plastic limit of a simple statically indeterminate I beam. The configuration of the beam is as follows

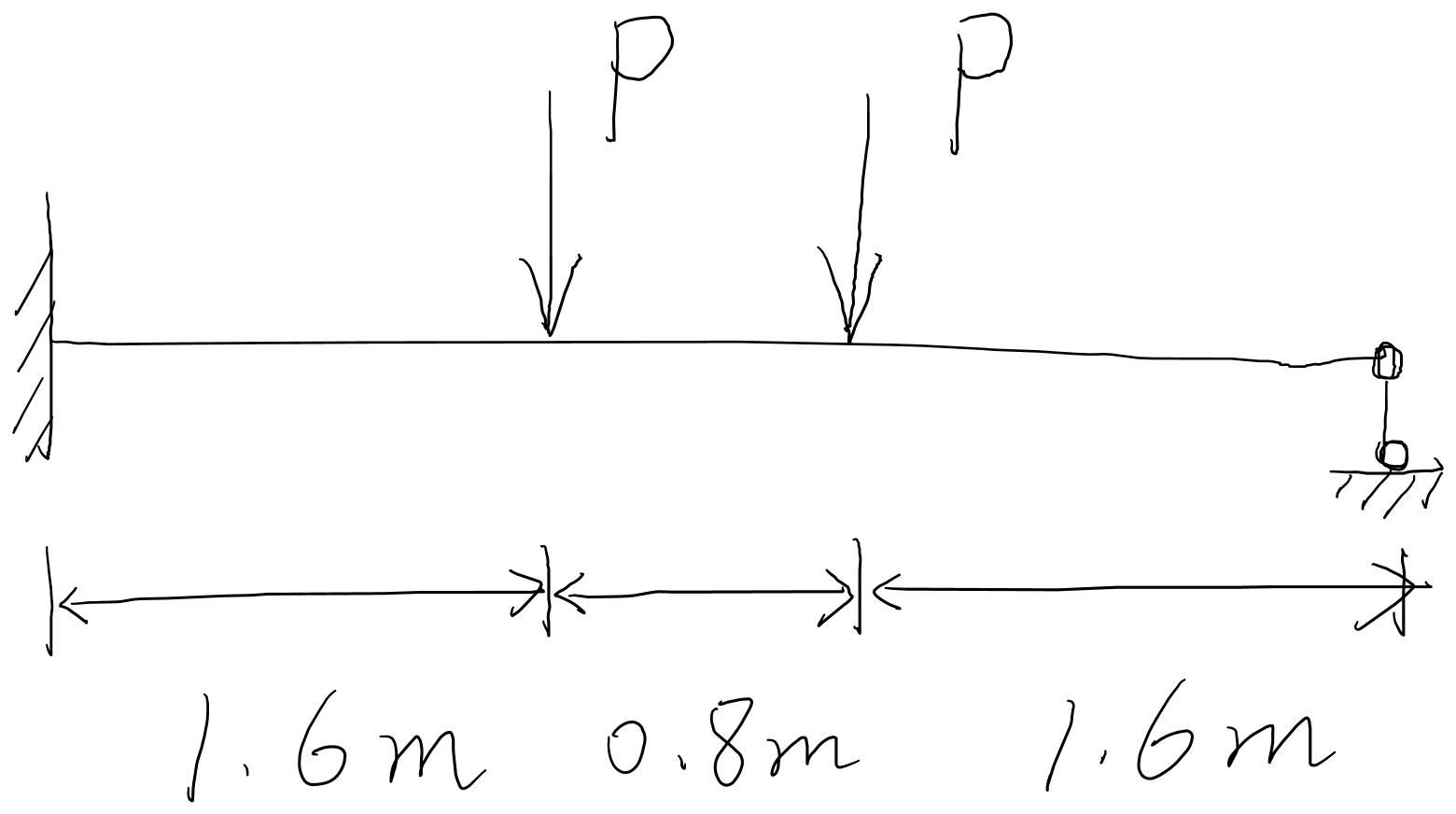
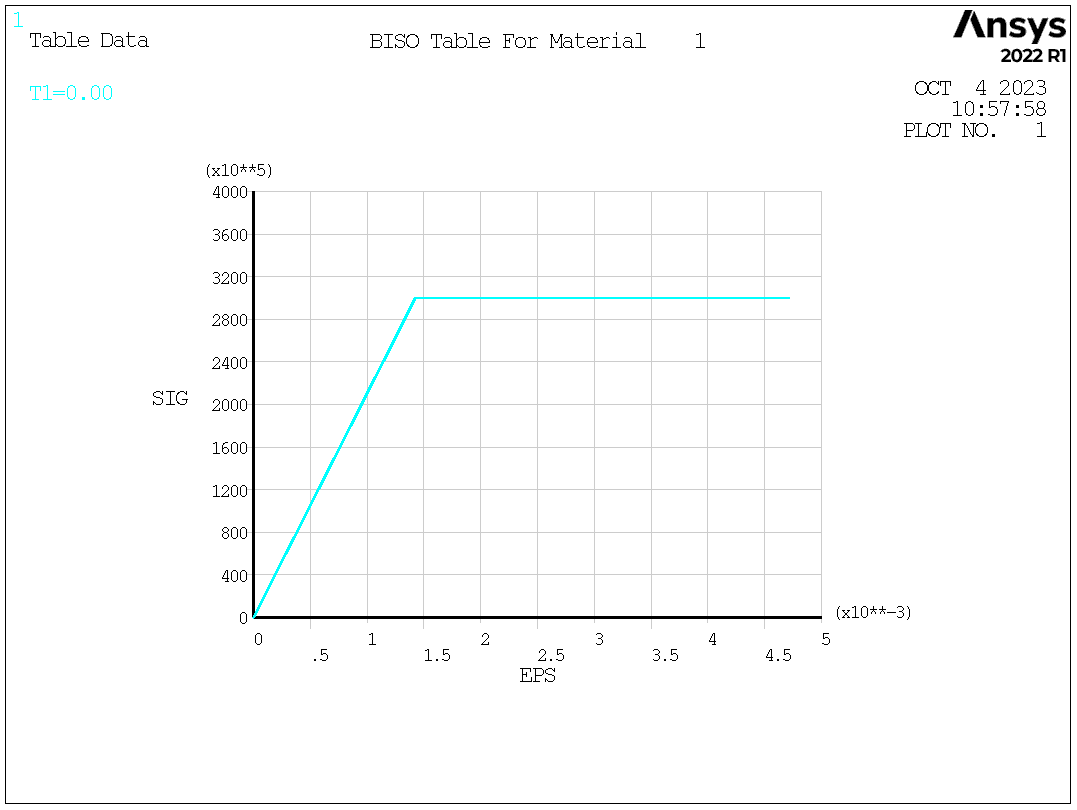
The material yield strength is 300MPa. The elastic modulus is 210GPa. The Poisson’s ratio is 0.3. Bilinear isotropic hardening (BISO) material model is used:

The cross-section of the I beam is as follows

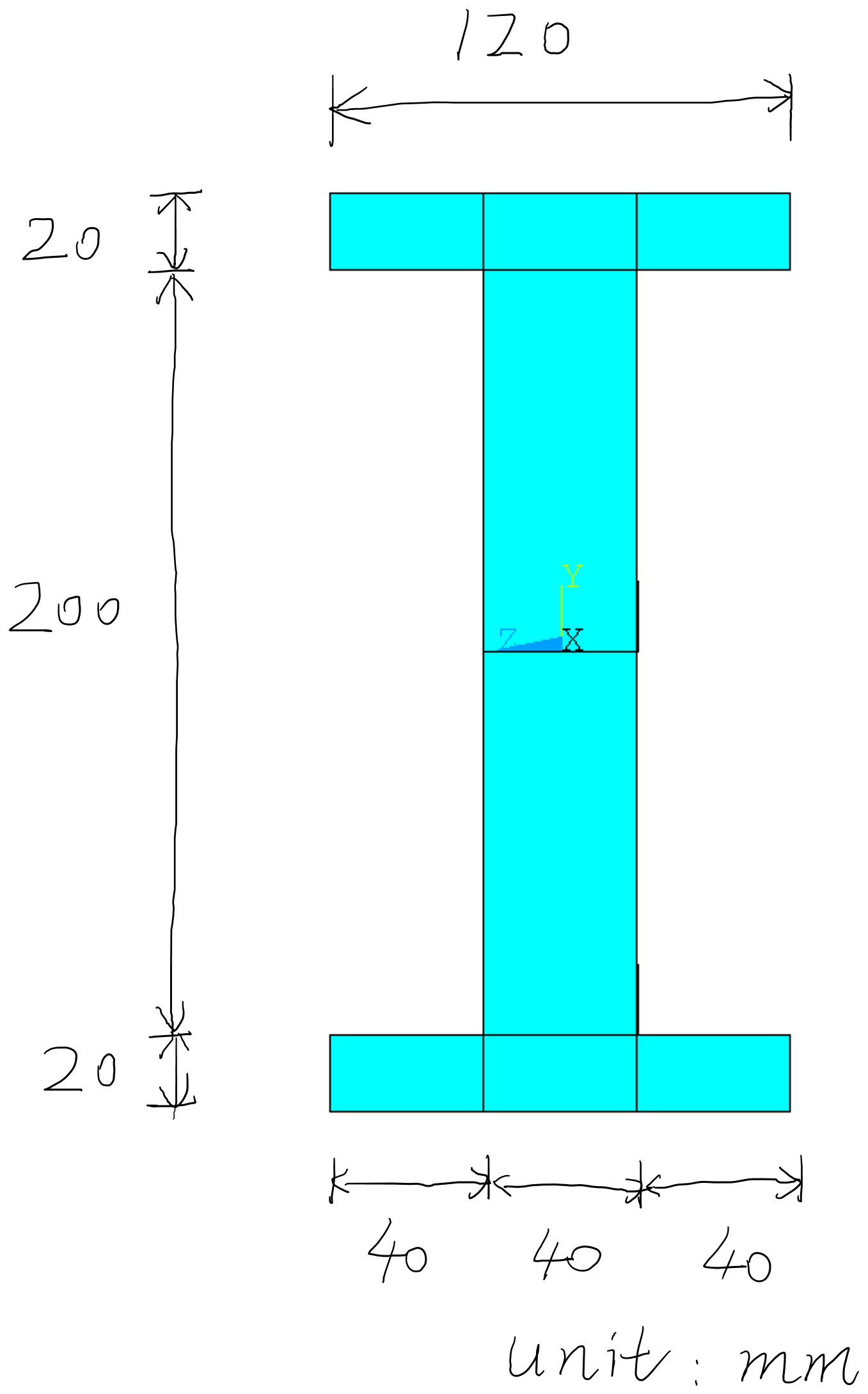
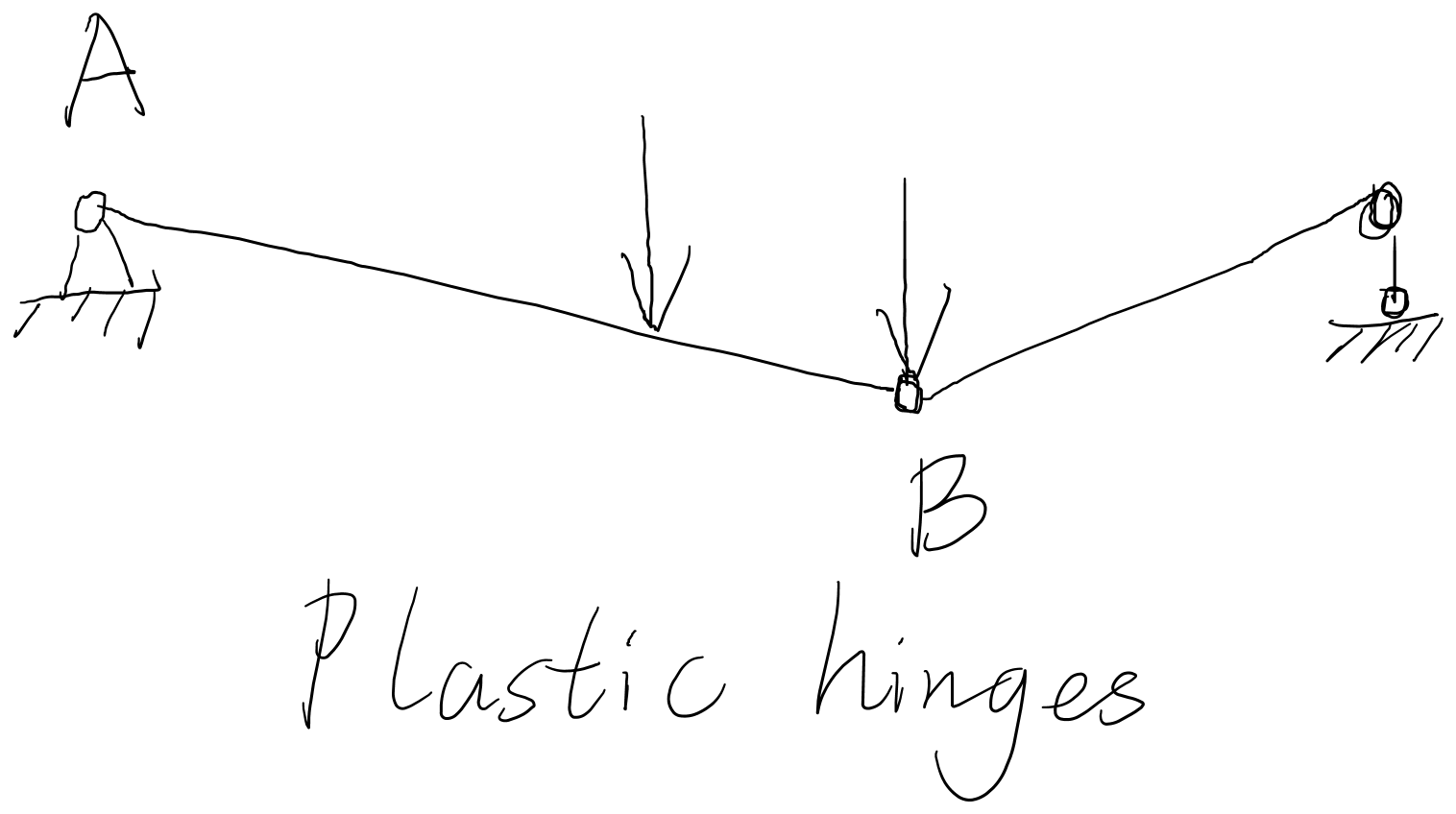
Based on hand calculation, the ultimate bending moment is 278.4kNm. When the beam reaches the plastic limit, there will be two plastic hinges (indicated by A and B in the following figure), which means the bending moment at A and B will be 278.4kNm. The ultimate load is 243.6kN.

Next the problem is solved using ANSYS. Some tips that deserve mentioning in this problem:

1. The beam is modeled using BEAM189, which is a 3D 3-node element based on Timoshenko beam theory. Due to the cross-section of the beam, one should be careful about the orientation of the beam, and hence the definition of an orientation node L.

2. Once the orientation of the beam is determined, make sure to export the correct bending moment (whether it is My or Mz) using ETABLE. It is determined using the element coordinate system.

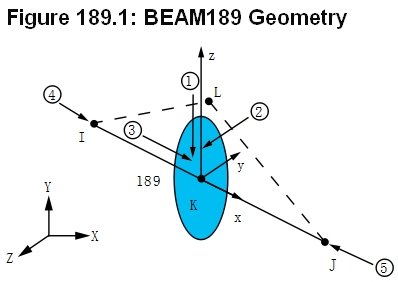
3. The applied load in ANSYS is a trial load based on initial estimation. It is possible that the analysis terminates itself due to excessive deformation before the final load is reached. In that case, the time data is essentially the percentage of the load that has been applied to the model. The penultimate load step represents the ultimate load step.

The APDL of this study is as follows (annotations are in lowercase)

FINISH
/CLEAR
/PREP7
P=260E3			!unit: N
ET,1,BEAM189
KEYOPT,1,7,1	        !Output control at section integration point
MP,EX,1,2.1E11
MP,PRXY,1,0.3
TB,BISO,1
TBDATA,1,300E6,0
TBPLOT,BISO,1
TBLIST,BISO,1
SECTYPE,1,BEAM,I
SECDATA,0.12,0.12,0.24,0.02,0.02,0.04
K,1
K,2,1.6
K,3,2.4
K,4,4
K,5,2,2
L,1,2
L,2,3
L,3,4
LATT,1,,1,,5,,1
LESIZE,ALL,0.1
LMESH,ALL
/ESHAPE,1
EPLOT
DK,1,ALL
DK,4,UY
FK,2,FY,-P
FK,3,FY,-P
FINISH
/SOLU
ANTYPE,STATIC
NLGEOM,ON
AUTOTS,ON
NSUBST,64
OUTRES,ALL,ALL
SOLVE
FINISH
/POST1
SET,LIST
SET,LAST
SET,PREVIOUS                    !check the penultimate load step
*GET,RTIME,ACTIVE,0,SET,TIME	!get the load associated with current load step
ETABLE,MI,SMISC,2               !bending moment My at node I
ETABLE,MJ,SMISC,15              !bending moment My at node J
PLLS,MI,MJ                      !plot bending moment diagram
! /CONTOUR,,9,0,,0.02
PLNSOL,EPPL,EQV                 !plot plastic zones
FINISH
/POST26
NSOL,2,64,U,Y
PROD,3,2,,,,,,-1000		!switch unit from m to mm
PROD,4,1,,,,,,P/1E3		!switch time variable to force in kN
/AXLAB,X,Node64 UY(mm)
/AXLAB,Y,P(kN)
PLTIME,0,RTIME			!Defines the time range for which data are to be displayed.
XVAR,3
PLVAR,4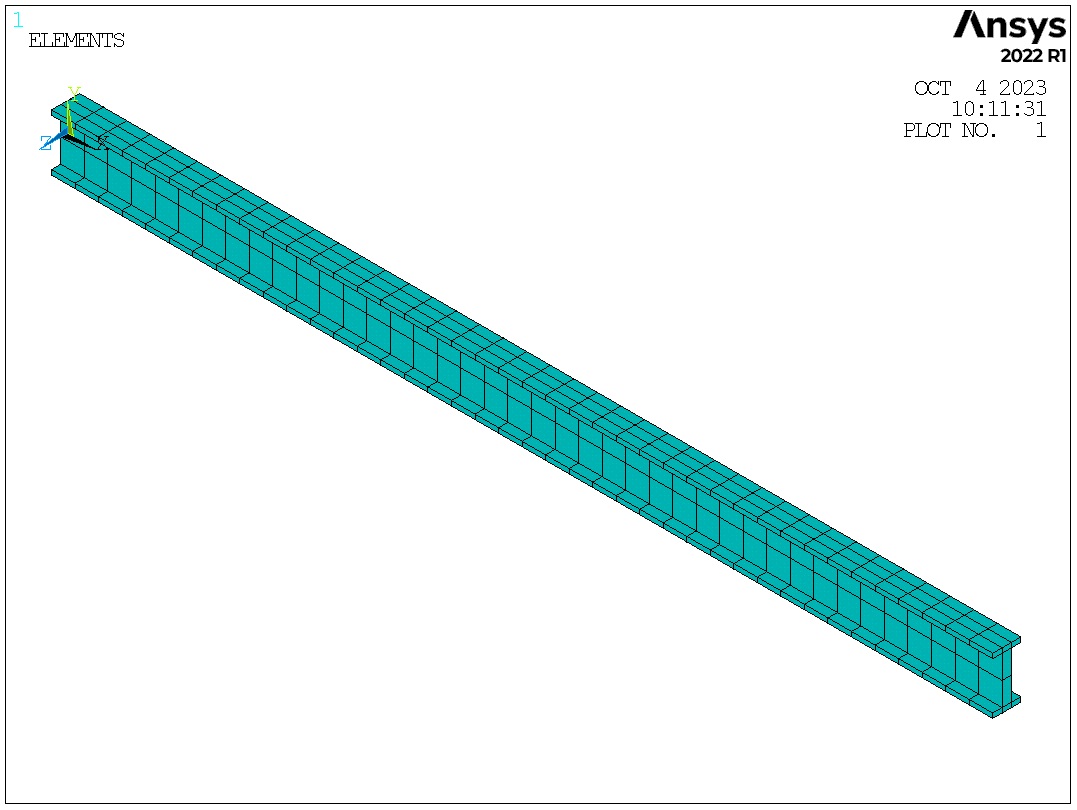

Beam elements.

When the load exceeds 246.764kN, error messages pop up:

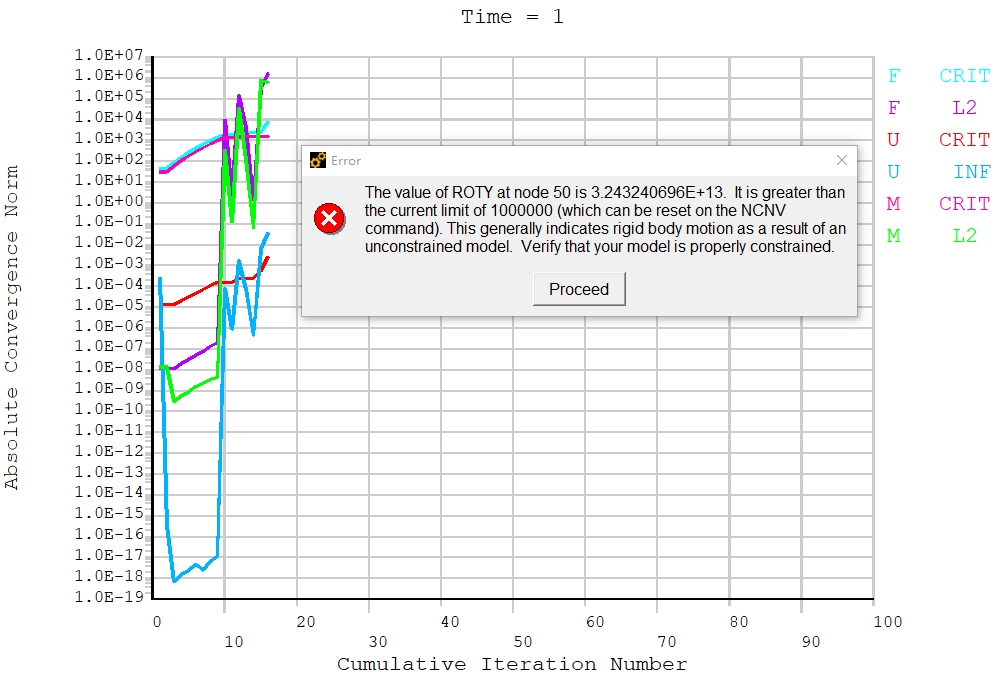
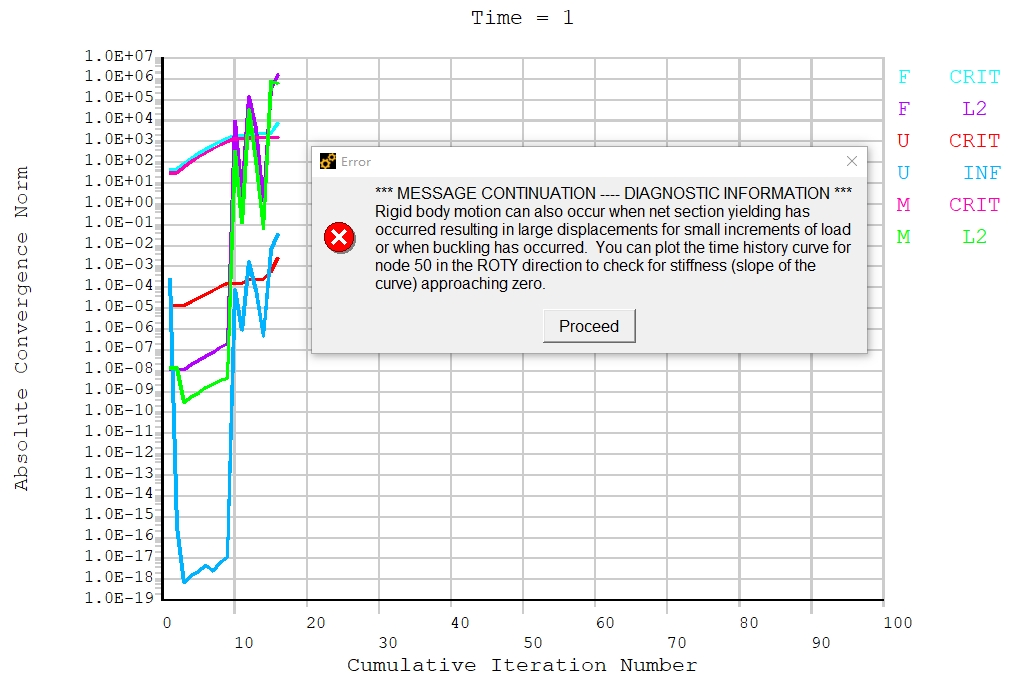
It means the ultimate load (i.e. 246.764kN) has been reached. Click proceed and the analysis will continue for a while, then results can be checked in postprocessor.

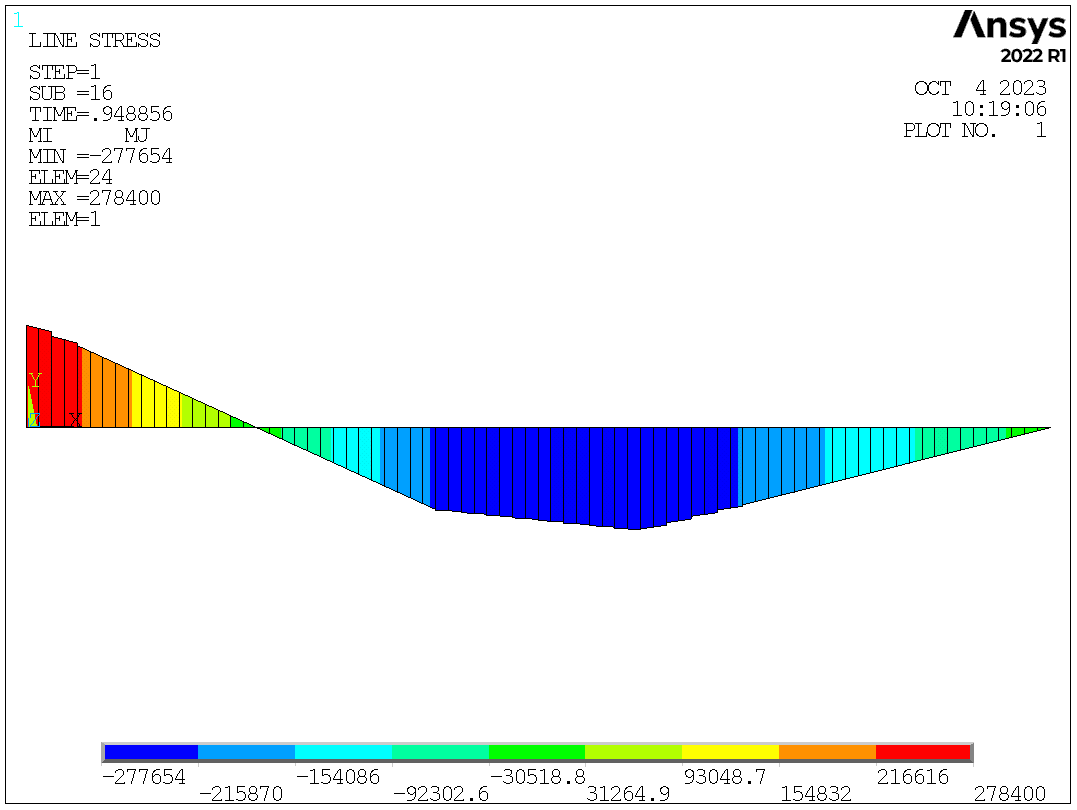
Bending moment diagram.

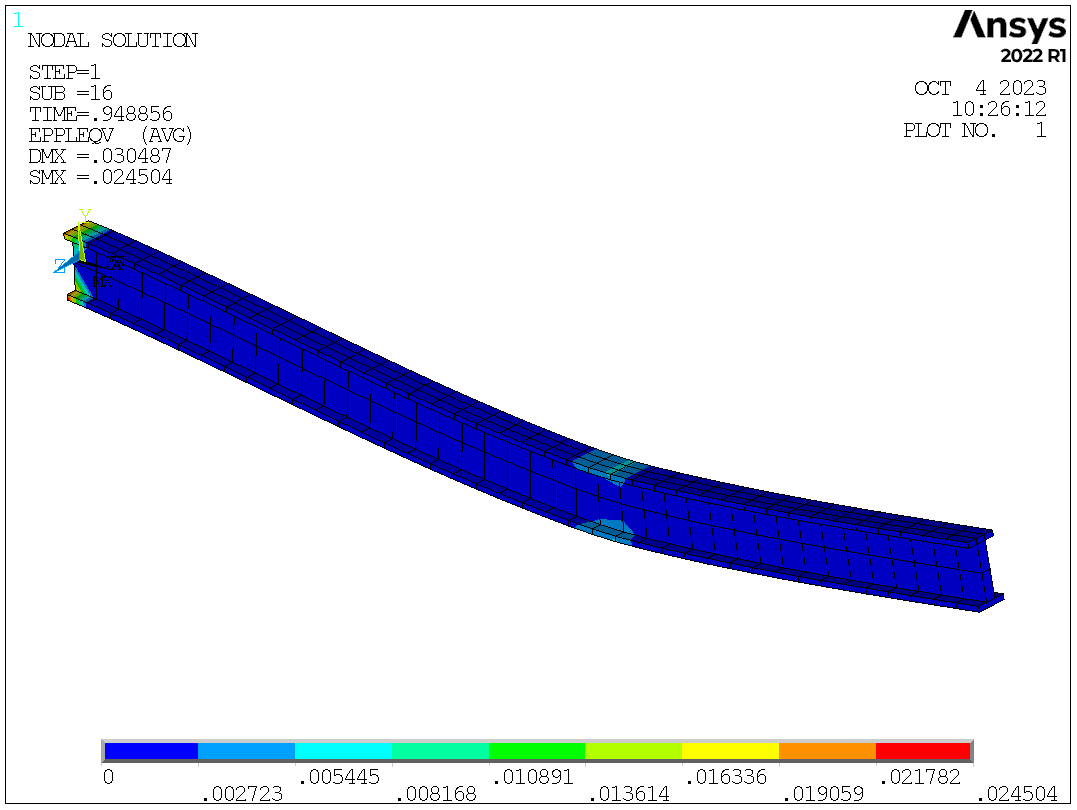
Plot plastic zones (equivalent plastic strain)

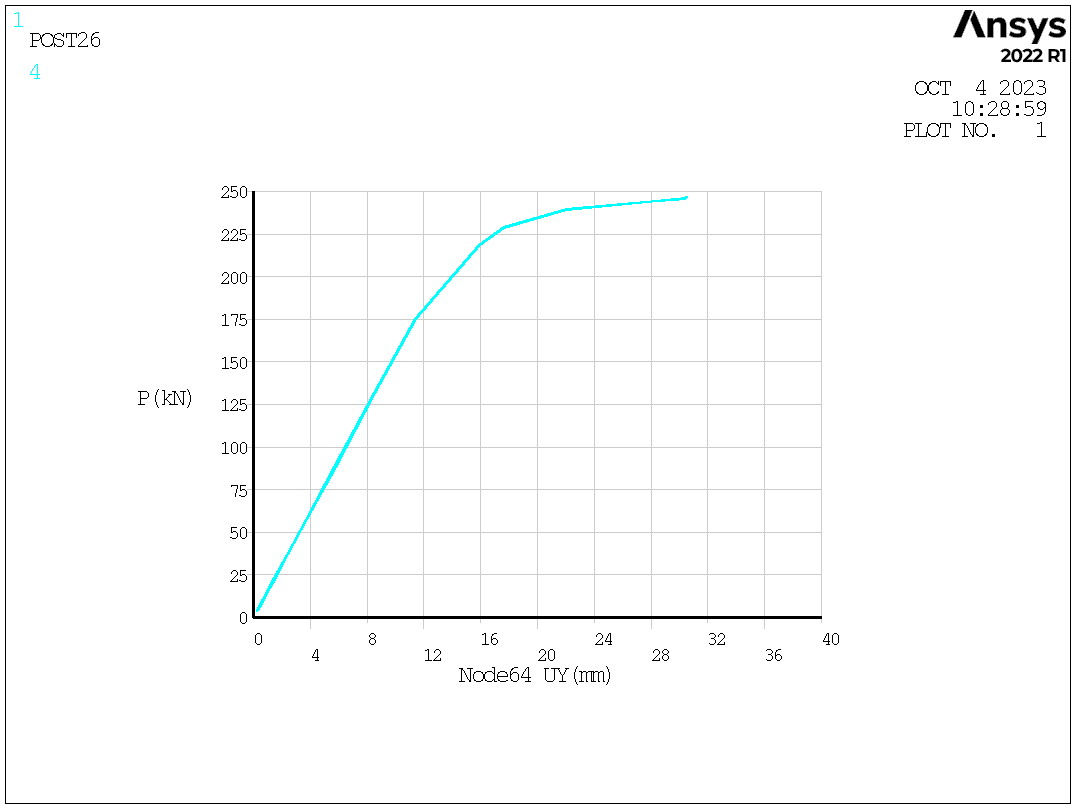
Equilibrium path.

The obtained ANSYS results are in good agreement with hand-calculated results. The position of plastic hinges can be observed. Using the equilibrium path, it is easy to tell when the model develops into the nonlinear stage.